確率 漸 化 式 は なお。 確率漸化式とは？問題の解き方をわかりやすく解説！

漸化式の応用(確率漸化式)

は 化 なお 確率 漸 式

あとはこの三項間漸化式を解くだけです。 問題2を解く上でのポイント まずは、文字設定を行っていきましょう。 問題1 正四面体と確率漸化式 の解答・解説 問題1の解答と解説を始めていきましょう！数学は適切な指針を立てられるようになることが最も重要ですから、 まず解説を書いてから、そのあと私が作ってみた模範解答を載せようと思います。

1656(確率漸化式(最初に注目～破産の確率))

は 化 なお 確率 漸 式

以前は「絶対にない」と断言していたのですが、2018年度東工大第5問で4種類の数列の連立漸化式を解かせる問題が出題されているとの情報をいただきました。 また、正四面体なので、対称性に着目すると良さそうです。 2000番台 数IIB• と合わせて となります。

18

確率漸化式、場合の数の漸化式の解き方を考察する 〜京大数学、漸化式の良問〜

は 化 なお 確率 漸 式

これは確率にも使えます。 しかし、この程度の問題文は短い方です。 上の遷移図からは、 という漸化式を立てることができますね。

2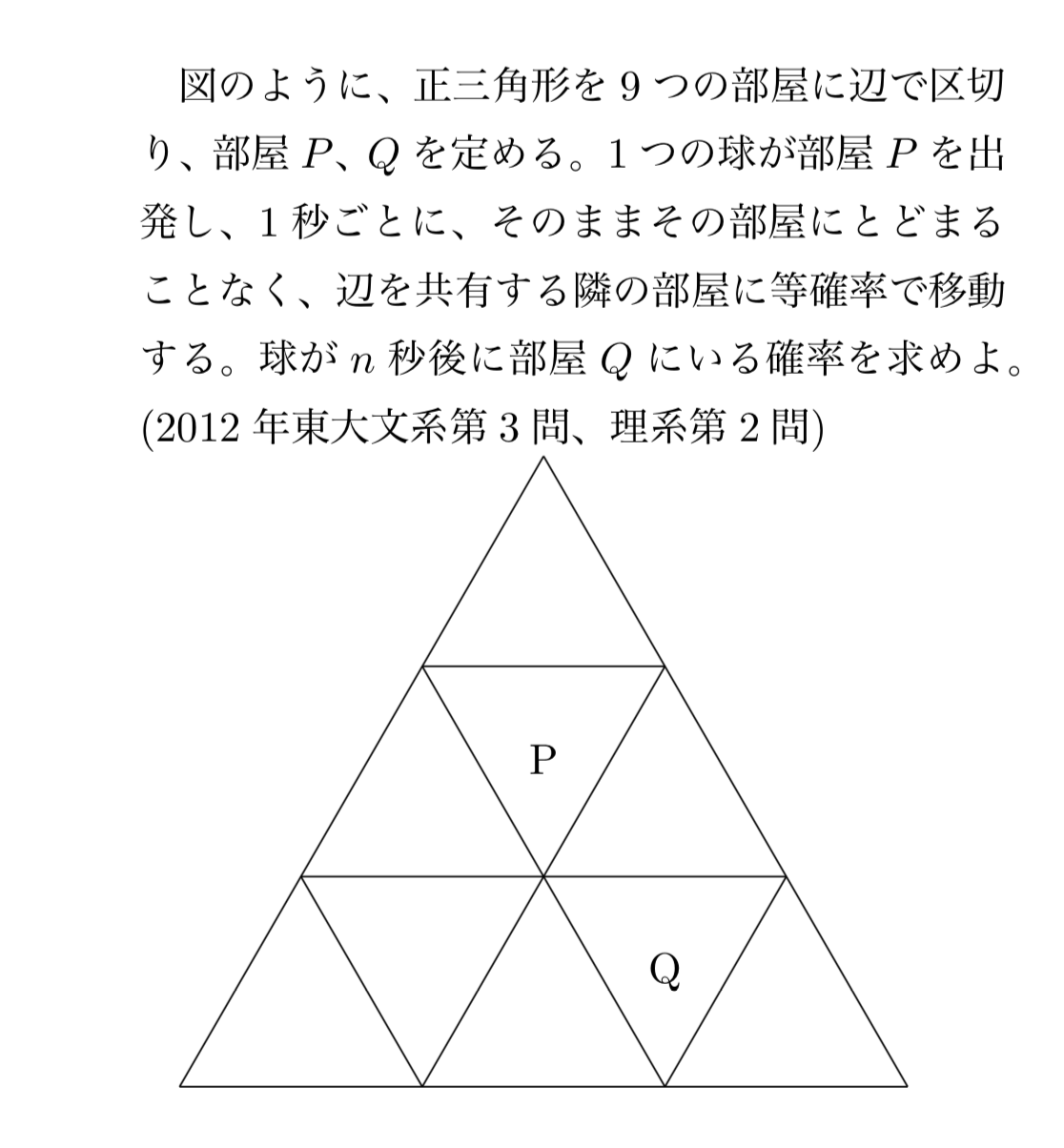

1656(確率漸化式(最初に注目～破産の確率))

は 化 なお 確率 漸 式

それでは、手順通りに解いていきましょう。 漸化式を攻略して周りの受験生に差をつけましょう！. これを元に漸化式を立てることができますね！ という漸化式が立つので、これを解いてあげればOKです。

8

漸化式の問題パターンと確率漸化式など典型的な解き方を徹底解説！

は 化 なお 確率 漸 式

確率漸化式とは？ 確率を求める過程で数列の漸化式が出てくるもの 確率漸化式とは、確率を求める上で出てくる、数列の分野で習う漸化式のことを指します。 問題出した方のセンスがおかしいと私は思う。 また、 ちょっとしたコツを知っておくだけで計算量を減らすことができて、結果的に計算ミスの防止に繋がります。

13

漸化式の問題パターンと確率漸化式など典型的な解き方を徹底解説！

は 化 なお 確率 漸 式

確率漸化式はもちろん、確率全般について網羅的に学べる良書です。 ある程度確率漸化式について学んでいるという人はこれらの問題を実際に解いてみましょう。 漸化式の解き方がまだあやふやだという人はこちらの記事で漸化式の解き方を学んでくださいね。

確率漸化式とは？問題の解き方をわかりやすく解説！

は 化 なお 確率 漸 式

Ｂｎ＋１の場合も同様に考えれば式をもう一本作ることができます。

19

確率漸化式とは?意味と解き方/推移図の描き方まで分かりやすく解説

は 化 なお 確率 漸 式

具体的には以下の様な推移図を書いていきます。 この記事では、東大で過去に出題された入試問題の良問を軸にして、確率漸化式の習得を目指します。 A ベストアンサー どんな文脈で出てきたのですか？ それが分からないと、何とも言えません。

20