円錐の体積

円錐の体積ってなんであの公式なの │ Webty Staff Blog

円柱の体積を求める問題問題1 図の円柱の体積を求めなさい。立方体だからこそ可能です。

もちろん、計算する場合には円周率をまとめるというような計算の工夫も行いましょう。例えば、三角形は高さが同じなら頂点を変えても、赤い幅が変わらないし、全体の面積も変わらない。

おうぎ形の面積は半径と中心角がわかれば求めることができます。

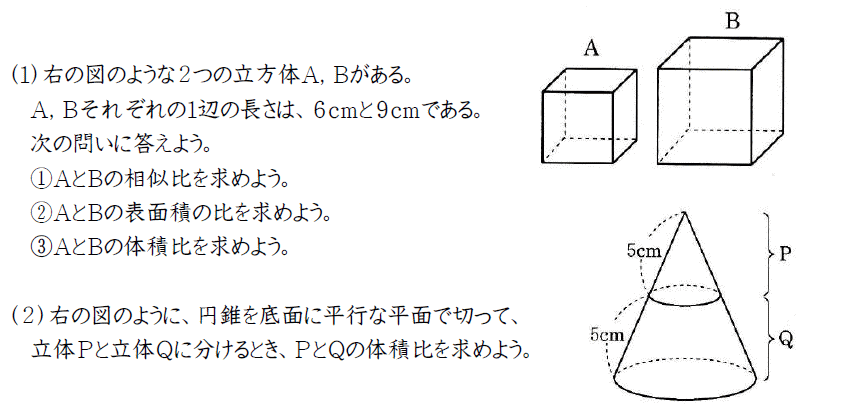
そうすると、以下のようになります。下図の円錐をみてください。では、錐体は底面積が２倍になったら、体積はどうなる？ S：底面積を２倍にした錐体を頂点から底面積が半分になるように切断します。

14として、それぞれの長さを求める公式に問題で与えられている数値を入れて式を作ると、次のようになります。円すいを広げて展開図にしたとき、側面はどのような形になっているでしょうか？上の図のように、円すいを広げると側面はおうぎ形になります。なお、円錐の表面積を出すときは少し考え方が複雑です。

ｙ＝ｘ 2の面積は正方形の１／３なんだ。半径が等しい扇形の面積は、弧の長さに比例する。 Contents• 少なくとも、小学校の算数や中学校の数学では証明することができません。

そのため、円周の長さ（おうぎ形の弧の長さ）は以下の計算によって出すことができます。

おわりにこれが出来たときは嬉しかったのですが、ノートを書いてみると地味ですね。上図の円錐では、底面積は以下になります。また下図の円錐の体積＝15m 3、半径＝2mのとき、高さを求めてください。