実格子と逆格子の対応 [物理のかぎしっぽ]
同じ名前にすることは出来るようですが、系列2のみを消すことは出来ないようです。
7
ただここまで詳しく説明する必要はないでしょう。
は で表されているため逆格子空間内の点 を指すベクトルである。 逆格子ベクトル・逆格子空間の意味 こいつらを初めてみるときは本当に意味不明だ。 ブリルアンゾーン [編集 ] 逆格子の単位胞は、逆格子の対称性を十分に反映していない。
4完全な対応(格子点の集合と集合の対応) ここまでは逆格子の点と平面群の対応の話でした. しかし,逆「格子」と言うからには, 一定の規則を持って整列した点の集合の対応物こそが, 重要な意味を持っているはずです.それを見てみます. 実はこの為に や を用意したのです. ここで逆格子の点 に対して, 対応する実格子の平面群を以下の様に名づけます. 例えば, ならば,対応1で求めた直線群を三次元に拡張した に 垂直な平面群です. ならば,対応2で求めた直線群を三次元に拡張した, 先ほどの半分の周期の に垂直な平面群です. 僕が主張したいことは, ではないかという事です. つまり,言葉で表現すると, まず特定の を持つ が異なる平面の集合を一つの図形 と考えます. (今, を固定しているので添え字を省略した.) そして,その後異なる に対して,その の共通部分を求めると, 実格子の格子点となっているだろうという事です. すみませんが,式 は証明はできていません. しかし,今まで具体的に見てきたように, が整数の組だった場合,実格子の上を 平面群 が漏らさず通る事から, ほぼ確実に成立するだろうと思います. さらに言えば, も成立するでしょう.なぜなら,格子点では が成立するので,式 の分数の値は となります.しかし,それ以外の点では,複素数の指数関数の位相がゼロではなくなり,その 倍周期を足していくことによって,ゼロになるはずです. それでは今日はこの辺で,お疲れ様でした.. 格子定数 AlN GaN InN 3. 2次元格子点のフーリエ変換 [編集 ] 3次元実空間中にある無限に続く2次元格子点は、次のように表される。 系列名の色を白にして見えなくする、プロットエリアのマーカーも二系列を同色とする、など考えられます。 一周期分積分しているところがミソである。
17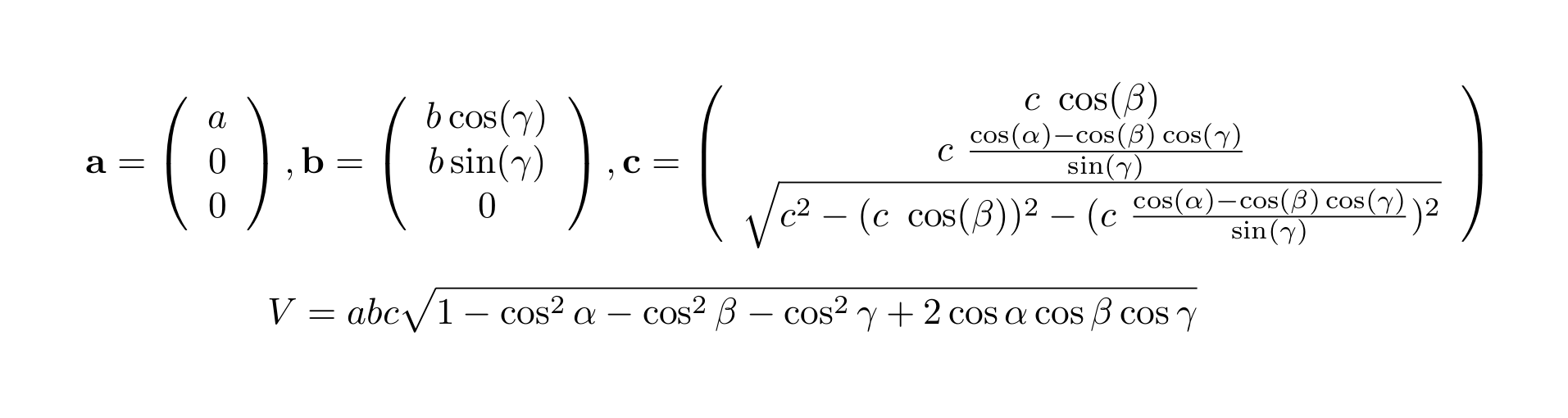
しかし、強いて、意味を考えるならば、塩化ナトリウムはナトリウムイオンと塩素イオンの2つの面心立方格子が重なった結晶だという見方ができます。
は で作られる平行六面体の体積である が互いに直交しているならば直方体、また、大きさが同じで直交しているならば立方体になる。 (2次元格子を考えて)) となります。 この平面は少なくとも一つの格子点を通過する必要があります。
9