無限 級数。 無限級数、無限等比級数とは？和の公式や求め方、図形問題

【基本】無限級数の収束・発散と項の極限

この も と同じように無限ですよね。 一般化 [ ] 漸近級数 [ ] ある種の関数のあるいはとは、定義域内の点における部分和がその関数のよい近似を与えるような無限級数をいう。 が発散する現象はオイラーによる素数の無限性の証明にも利用されている。

16

無限等比級数の収束，発散の条件と証明など

もちろん、「１＝２」なんてのはあり得ませんので、この証明はどこかが必ず間違っています。

8

無限級数、無限等比級数とは？和の公式や求め方、図形問題

級数に和の値が結び付けられているとき、しばしば便宜的に「級数の和の値」の意味で「級数」という言葉を用いることがある（和の値を単に和と呼ぶことがあるのと同様である）。 以上をまとめると次の公式が得られる。 今までの延長でスラスラ理解できると思いますが途中で区切るところもあまりなく長文になってしまいました。

級数

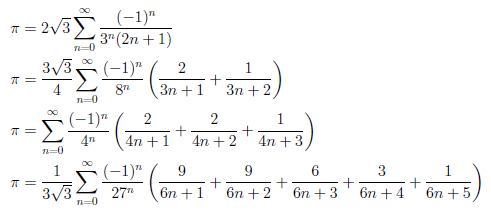
では をとてつもなく大きな数にしたら はどうなるでしょうか? 証明3．積分を用いる方法 無限級数の評価で積分を用いるのは定石です。 発散級数 [ ] 詳細は「」を参照 「通常の意味」での和が収束しないような級数に対して、何らかの意味で和と呼ぶにふさわしい極限値を割り当てることができるというような状況はたくさんある。 ここからは、種明かしをしていきたいと思います。

4

無限級数の求め方 ｜ 数学の偏差値を上げて合格を目指す

よって、無限級数は発散する。

11

無限等比級数の収束，発散の条件と証明など

しかし、その多くは、結局その証明の途中で、0で割るなどの初歩的な反則をしていて、少し数学がわかる人なら簡単に見破れるものがが多いです。

2

無限級数とは 部分和で無限級数の極限を考える

級数の収束性 [ ] によって項が添字づけられている場合にはととの2つの収束性の概念を定義することができる。 収束冪級数の収束はその収束域において一様で、各項の冪関数は可積分かつ連続的微分可能であるから、収束冪級数は項別積分可能かつ項別微分可能であり、その原始関数および導関数はもとの冪級数と同じ収束域もつ冪級数として得られる。

3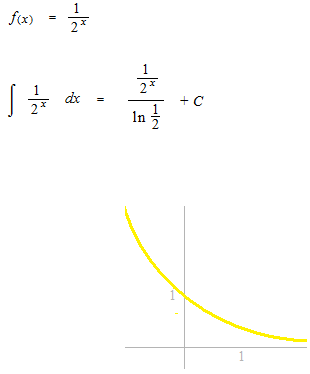

【無限級数】の定義と、収束・発散を調べるためのコツをまとめました。

位相アーベル群 X がである場合には、族 a が X において無条件総和可能であることと、後述する「コーシーネット条件」を満たすことがになる。 ですが何度もいうように極限は数学において非常に重要な概念であり、証明されている操作です。 でも何をしたらいいのかさっぱりわからない. を項に持つ関数項級数の一様収束極限に対する 項別微分可能性も同様である。

7

無限級数の求め方 ｜ 数学の偏差値を上げて合格を目指す

間違いの無いよう気を付けて書いておりますが、もし、あれ？これ間違ってね？って思った方がいれば、それはきっとこの記事が間違っています。 しかし、この記事で紹介する「１＝２」の証明は、そのような 安っぽいハッタリとは一味違います。