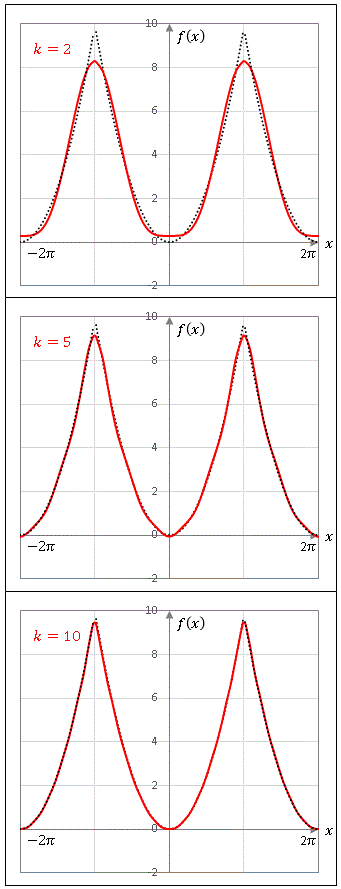
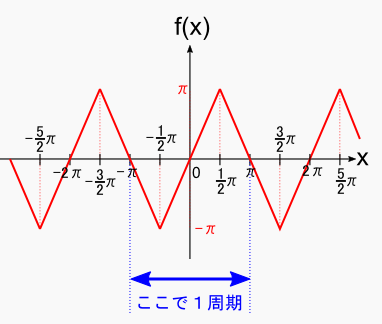
フーリエ級数展開式の導出と矩形波・鋸波のフーリエ係数の計算
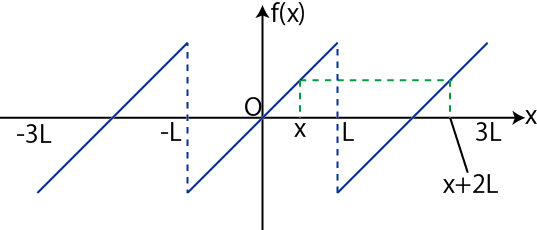
しかし、世界を見ると 周期的な動きを見せるものが非常に多いことに気づくはずです。 少なくとも証明を知らないとフーリエ級数展開を使ってはいけない, という決まりはありませんので, 優先度は低いと思います. 色をつけて公式を少しわかりやすくしてみました! つまり、周期関数 を 偶関数 , , , …… と奇関数 , , , …… を用いて表せるよってことなのです! 少し難しい用語を使うと、周期関数 を偶関数 , , , …… と奇関数 , , , …… の 1次結合で表せるってことです! しかし、フーリエ係数 , の求め方が複雑だったりなぜか初期値が となってたり がなかったりしますね。
7