【3分で分かる!】三角関数の合成公式の証明と使い方のコツをわかりやすく
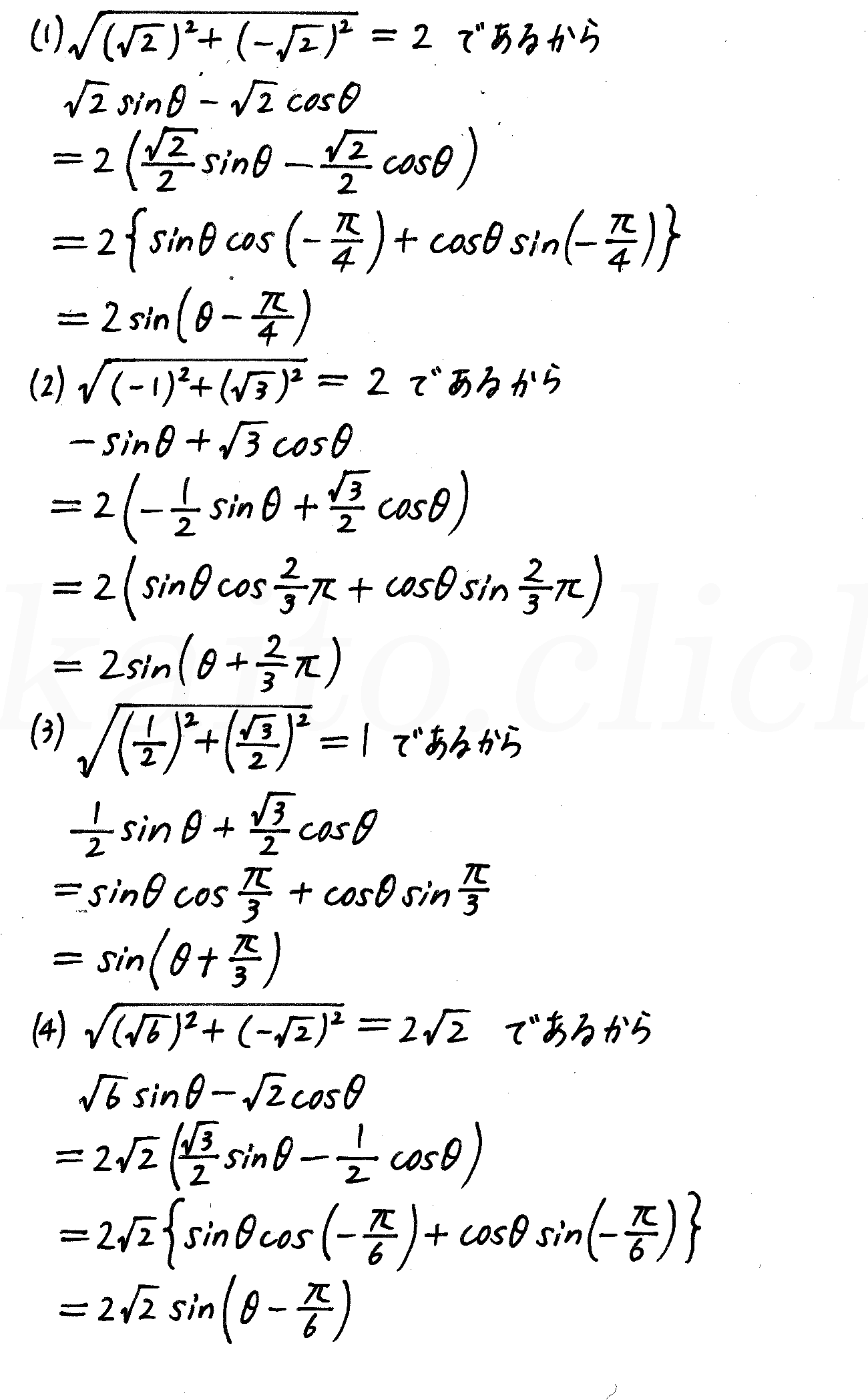
三角関数の合成は複数の波を1つの波として、サインで統一して表すためのもの。 もちろん我々がこれからやることは、その逆、 「左辺のバラバラの三角関数を合成して、右辺を作り出すこと」 です。 答え:. 三角関数の最大最小ってそんなに多くないからこの形は必ず覚えておこう。
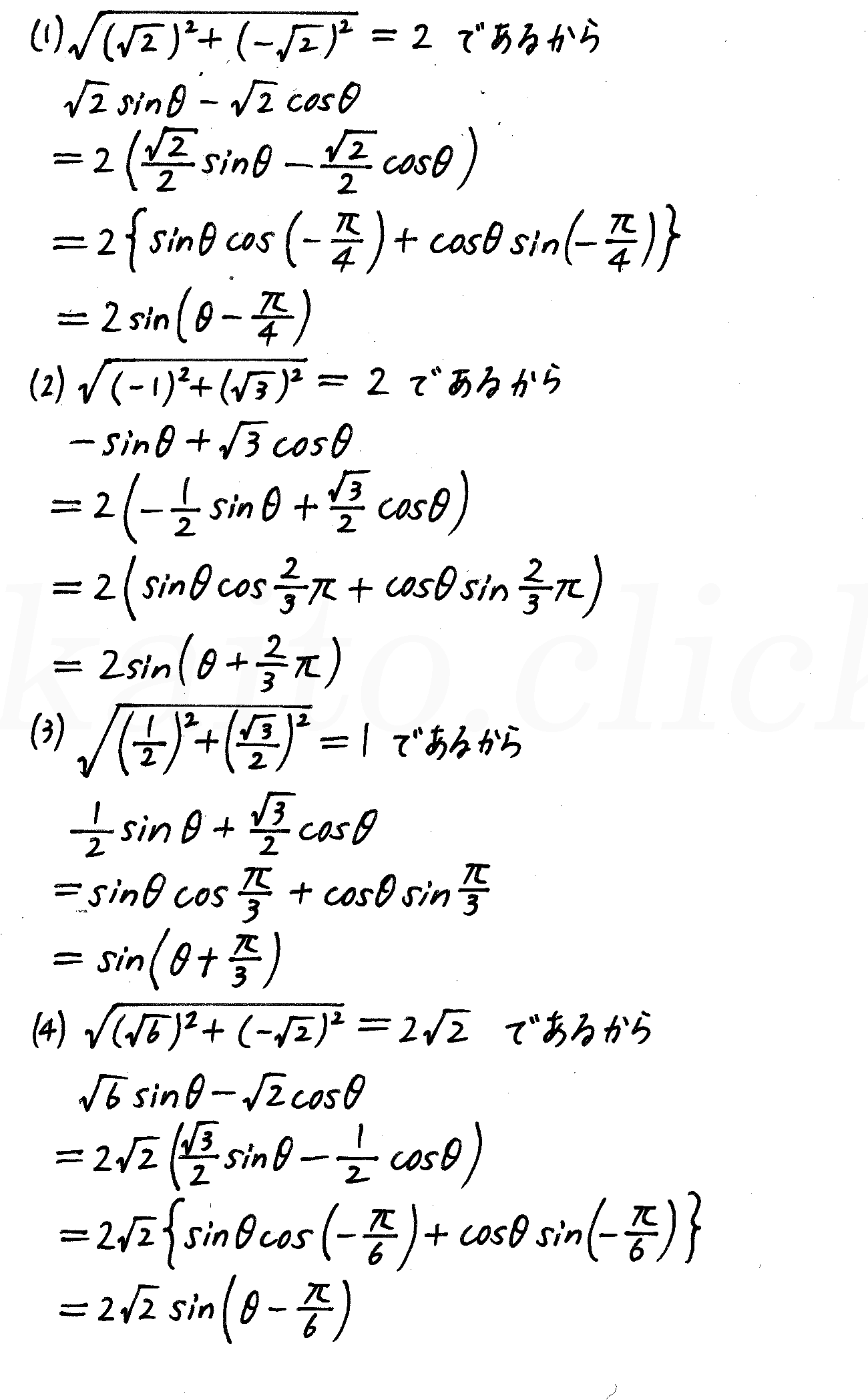
三角関数の合成は複数の波を1つの波として、サインで統一して表すためのもの。 もちろん我々がこれからやることは、その逆、 「左辺のバラバラの三角関数を合成して、右辺を作り出すこと」 です。 答え:. 三角関数の最大最小ってそんなに多くないからこの形は必ず覚えておこう。

どちらかお一人がお手続きするだけでOKです。 「旧帝大」とは、北海道大、東北大、東京大、名古屋大、京都大、大阪大、九州大のこと、「早慶上理」とは、早稲田大、慶應義塾大、上智大、東京理科大のこと、「MARCHG」とは、明治大、青山学院大、立教大、中央大、法政大、学習院大のこと、「関関同立」とは、関西大、関西学院大、同志社大、立命館大のこと、「日東駒専」とは、日本大、東洋大、駒澤大、専修大のこと、「産近甲龍」とは、京都産業大、近畿大、甲南大、龍谷大のことです。
2
三角関数では「加法定理」か「合成」は確実に使います。 合成はなぜ必要か 三角関数には2倍角や半角の公式の他に使い勝手の良いもう一つの公式があります。
19
2019年12月17日に2021年度「大学入学共通テスト」にて予定されていた国語・数学の記述式問題の導入見送りの発表が文部科学省よりございました。 合成は正弦(サイン)でできれば十分です。

問題作成者はどうやってこの問題を作っているかというと、 答えを先に決めます。 この問題では となります。 ここから,この 2 つの値を と の値として取る角 こちらは 【 Point Pickup 】 では とおいています が求められます。
ちなみに、cos の形に合成することを考えると、の内積として見ることもできますね…。 もちろん書かずに合成できるようになればかまいませんが、 加法定理を利用するので書いた方が最終的には広く使えるようになります。 実はこの方法は応用問題で頻出の大事な内容ですし、どうやって作ったかがかなり重要なので自分で作れるようにしておくと良いです。
12
特徴的な式の形とは以下のようなものです。 つまり同じ値になるってことだからね。 暗記するだけじゃ全く使い道がわからなかったものが、意味を考えると何をすればいいか見えてくるでしょう? テスト前は暗記でもいいですが、普段勉強するときは暗記よりも意味を意識してみてくださいね。
2